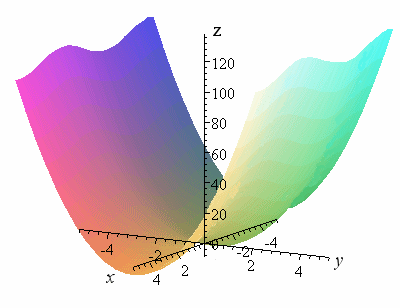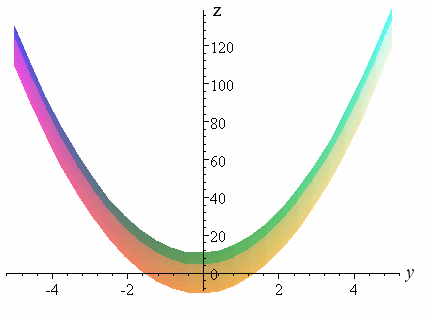10. Partial Derivatives

by M. Bourne

So far in this chapter we have dealt with functions of single variables only. However, many functions in mathematics involve 2 or more variables. In this section we see how to find derivatives of functions of more than 1 variable.

This section is related to, but is not the same as Implicit Differentiation that we met earlier.

Example 1 - Function of 2 variables

Here is a function of 2 variables, x and y:

F(x,y) = y + 6 sin x + 5y²

To plot such a function we need to use a 3-dimensional co-ordinate system.

Partial Differentiation with respect to x

"Partial derivative with respect to x" means "regard all other letters as constants, and just differentiate the x parts".

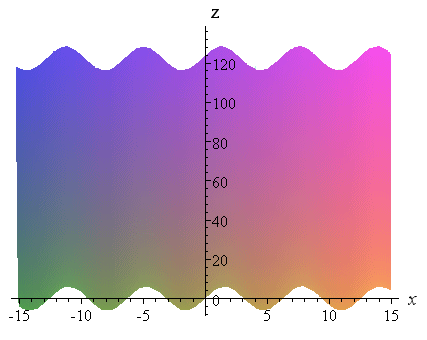
In our example (and likewise for every 2-variable function), this means that (in effect) we should turn around our graph and look at it from the far end of the y-axis. We are looking at the x-z plane only.

We see a sine curve along the x-axis and this comes from the "6 sin x" part of our function F(x,y) = y + 6 sin x + 5y². The y parts are regarded as constants (in fact, 0 in this case).

Now for the partial derivative of

F(x,y) = y + 6 sin x + 5y²

with respect to x:

`(del F)/(del x)=6 cos x`

The derivative of the 6 sin x part is 6 cos x. The derivative of the y-parts is zero since they are regarded as constants.

Notice that we use the curly symbol ∂ to denote "partial differentiation", rather than "`d`" which we use for normal differentiation.

NOTE: You can explore this example using this 3D interactive applet in the Vectors chapter. In the drop-down list of examples, this is the last one.

Partial Differentiation with respect to y

The expression

Partial derivative with respect to y

means

"Regard all other letters as constants, just differentiate the y parts".

As we did above, we turn around our graph and look at it from the far end of the x-axis. So we see (and consider things from) the y-z plane only. (Notice the horizontal axis on the following graph is labeled y, not x.)

We see a parabola. This comes from the y² and y terms in F(x,y) = y + 6 sin x + 5y². The "6 sin x" part is now regarded as a constant. (It actually has the effect of moving the base of the parabola `z=y+5y^2` down by 6 units.)

Now for the partial derivative of

F(x,y) = y + 6 sin x + 5y²

with respect to y.

`(delF)/(dely)=1+10y`

The derivative of the y-parts with respect to y is 1 + 10y. The derivative of the 6 sin x part is zero since it is regarded as a constant when we are differentiating with respect to y.

NOTE: Once again, you can explore this particular example (rotate it, view it from different axes, etc) using the 3D interactive applet in the Vectors chapter. In the drop-down list of examples, select the last one.

Second Order Partial Derivatives

We can find 4 different second-order partial derviatives. Let's see how this works with an example.

Example 2

For the function we used above, F(x,y) = y + 6 sin x + 5y², find each of the following:

(a) `(del^2F)/(delydelx)`

Answer

(b) `(del^2F)/(delxdely)`

Answer

(c) `(del^2F)/(delx^2)`

Answer

(d) `(del^2F)/(dely^2)`

Answer