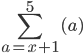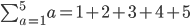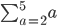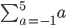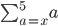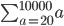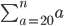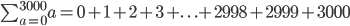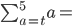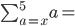Summation notation
By Murray Bourne, 15 Jun 2010
I had the following exchange with a reader over the last few weeks.
It's long (over 2 parts), but if you want to understand summation notation, it's worth reading!
This post also demonstrates the Socratic Approach to math teaching, where the teacher gives space for the learner to figure things out for themselves.
The exchange was done entirely in Google Docs and I have just pasted it here.
Note how respectful Yousuf is. I don't mind helping him at all as he is willing to show his appreciation at every step. Sadly, not everyone responds like this.
My replies throughout are in bold.
Yousuf asks:
Hi again sir
Thanks for reading this sir, I greatly appreciate your kind support.
Sir, this is the very last question on that exercise on sequences. This one's a lot different and I've a feeling it's going to be a lot more difficult especially considering the way it's written.
The question is ...
14. Given that:
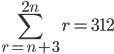
find the value of n.
OK the expression's turned out kind of unusually, but just to confirm:
The 2n is supposed to above the sigma sign and the r=n+3 part is supposed to be below it.
I don't understand anything about this particular expression and if it's got anything to do with that previous thing we did about those sigma equations, I have no idea what to do here sir!
I'd be very grateful if you could please help me on this one sir
Thanks again sir, I really appreciate your time 🙂
Yousuf.
Me:
OK. First question - write out what this means:
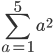
This will help: Helpful revision
Hi again sir,
It just means ...
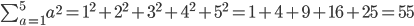
Thanks sir
Yousuf
Correct.
OK, next, what is
Hi again sir,
Would it be ...
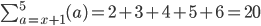 ???????????????
???????????????
Thanks 🙂
Yousuf
Where did your 2 come from?? And how do you know it is 5 terms?
Go back to the first example, which you did properly. It said "start at a=1" at the bottom of the Sum sign, which you did. You substituted in 1 and got 1^2.
Then you added 1 and got 2, and substituted that in and got 2^2
You stopped when you got to 5, since that is on the top of the Sum sign.
Now, go back to my second question and start where it says to start, and finish where it says to finish.
Hi again sir
Mmmm....I first thought that we always start with 1, but it seems I'm wrong clearly.
If we start at a = x+1, would it then be ...
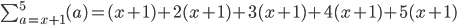
And terminate at 5(x+1) since it's the last one?
Thanks again sir 🙂
Yousuf
We are getting somewhere, but it's not quite right yet.
1. There is no MULTIPLY in the question, so why are you multiplying?
2. The number at the top is 5, so that should be the last number.
3. Once again, you have 5 terms. How do you know it is 5 terms?
Pls read my summary above about the things you did right before.
Try again ^_^
Sorry sir, but I have no idea. I'm always thinking we start off with a = 1 in all these sequences, but again I have no idea what to do here.
Right, I think the first term would definately be ...
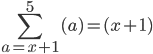
Because we substitute a = x+1 into (a). But how do we get to 5?
What I did in the last example was that I subbed a = 1 into (a^2) and followed throughout using the natural numbers 1, 2, 3, 4 and 5 (with 5 being the last one).
This one's confusing because it's x+1 which I'm not sure if I am to use the natural numbers, then this means it'll be 2, 4, 6, 8, 10???
Yousuf.
This bit you said is quite correct:
What I did in the last example was that I subbed a = 1 into (a^2) and followed throughout using the natural numbers 1, 2, 3, 4 and 5 (with 5 being the last one).
And what you did above was correct, starting with (x + 1).
(1) For the second term: add 1 to (x + 1)
(2) For the 3rd term: add 1 again, and so on.
(3) As I have hinted several times, there is not (necessarily) 5 terms
(4) What is the last term?
Hi again sir
Thanks for replying back sir 🙂
But I thought the number above sigma indicates the number of terms (so in the case of
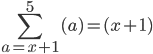 ,
,
there should be 5 terms in the sequence shouldn't there???)
The textbook I have says this and also says if its infinity instead of 5, for example, then the sequence goes on and on. But the number above sigma essentially means there's a restriction to the number of terms in that sequence doesn't it??
But even then sir, if
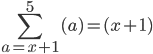
then wouldn't the second term be a + (x+1), like ...
![\sum_{a=x+1}^{5}{(a)} = (x+1)+[(x+1)+(x+1)]+[(x+1)+(x+1)+(x+1)] \ . \ . \ .](/blog/wp-content/images/2010/06/images/EXTERN_0007.png)
... since we're adding on (x+1) because a = (x+1)??
Sorry sir, but this is the first time I've come across an expression of this kind and I'm sure it's covered in the pure algebra units after (actually I just checked in the books and it isn't)!
Sorry sir, but could you please explain what is meant by the part ![]() and if you do substitute this into a, do you then always (including for all other related expressions under sigma) add 1 all the time??
and if you do substitute this into a, do you then always (including for all other related expressions under sigma) add 1 all the time??
The only thing I do have in the textbooks similar to this is this ...
And still, I don't know what's going on.
Thanks again sir, and I'm really sorry I hope you can understand this is the first time I've come across something like this. The textbook has concentrated on an isolated value of a throughout.
Thanks again sir 🙂
Yousuf.
No need to apologise! You are right - this is the first time you are coming across this.
But please realise - in the "real world" we come across novel problems and what we need to do is to apply what we already know.
That's what they are trying to do here - get you to apply what you know in a novel situation.
Your answer above is getting closer, but still not quite. You have added (x + 1), each time, not "1" as it should be.
I can understand why that textbook example didn't help at all!! Yet another case where they just assume you can figure it out.
OK - back to the problem.
It will only be 5 terms if you have a simple case like the one I gave you earlier. Only one variable is involved (a), and so there are 5 terms.
In summary, write the first number given at the bottom, add one to it then add that to the first number given, then add 1 again, add that to the other 2 already there.
That's our process, whether we know an actual value for the first term or not.
Question - is there an "a" in my expansion above?
Now, try to expand these ones. I hope they lead you to enlightenment!
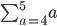
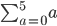
Were there 5 terms for each of the above? Did "a" appear in any of your answers?
The above 2 answers should be almost identical, except for the letters you use. HINT: There will be no "a" in the answer.
Now try this one again:
Hi sir
Thanks for reading this, and I'm sorry for not having replied back sooner.
Right, I'll give each one a go...
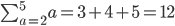
substituting values from a = 2 to a = 5
Correct - finishes when a = 5. There are 3 terms only in the series (not 5).
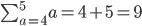
substituting values from a = 4 to a = 5
Correct - finishes when a = 5. There are 2 terms only in the series (not 5).
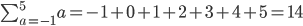
substituing values from a = -1 to a = 5
Correct - finishes when a = 5. There are 7 terms in the series (not 5).
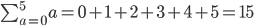
substituting values from a = 0 to a = 5
Correct - finishes when a = 5. There are 6 terms in the series (not 5)
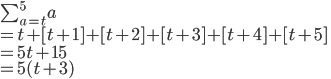
...subbing values from a = t to a = t + 4
The last term has to be [t+4] because if a = 1, then the last term would be 5, in that [4+1] = [5].
NOT correct - you have not finished with a = 5. Why are there 5 terms in your series? I keep hinting there will NOT be 5 terms in the series!! (The start is correct)
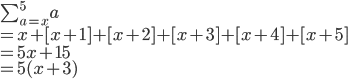
... subbing values from a = x to a = x+4
The same condition would apply here also as said before.
NOT correct - you have not finished with a = 5, again. Why are there 5 terms in your series? (The start is correct)
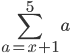
The expression itself is saying that the first number, a, will be such that it will be +1 that of the first term, namely 1.
[NO - this is not what it is saying. Look at your correct patterns above!]
For this one, what I plan to do is to start with the number 2 since a = x + 1, then the first term would be 2 as a = (1) + 1 = 2. The last term would then be 5 since a requires the sequence of natural numbers, therefore ...
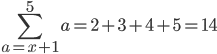
NOT correct - you have not started correctly, using the correct pattern from above. But yay - we don't have 5 terms in the series!!
Did I do those OK sir?
Thanks so much sir 🙂
Yousuf.
Hi again sir
I'll give it another go...
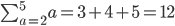
In this example, what I did was that I substituted a = 2 as the first term, and then continued using the natural numbers until I reached a = 5.
In the case of ...
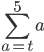
... what I think it is saying is that the first term is a = t and the series will end when we reach a = 5.
But you didn't start with 2 above! What you wrote above is correct, but none of the following expansions is correct.
(I know this is going to be wrong sir) Does that mean it will appear as ...
![\sum_{a=t}^{5}a=t+[t+1]+[t+2]+[t+3]+[t+4]+[t+5]=5t+15=5(t+3)](/blog/wp-content/images/2010/06/images/EXTERN_0024.png)
or would it be ...
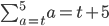
since the first term is a = t and the last term is a = 5???
Also, would the next one be...
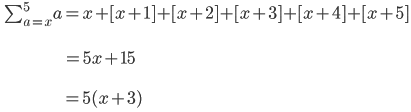
or would it be ...
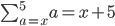 (since the first term is a = x and the last term is a = 5???)
(since the first term is a = x and the last term is a = 5???)
OK since that is that done (hopefully right)...
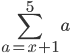
IN all honestly sir, I still don't know what it's asking. Is this going to be an algebraic sequence if it's not numeric?
Because I don't understand that if a = x+1, then what will this number be? I first thought it'd be 2, but if it's algebraic, then wouldn't it be (x+1).
If it's (x+1), then shouldn't the next terms be ...
(x+1) + 1
(x+1) + 2
(x+1) + 3
(x+1) + 4
(x+1) + 5
So
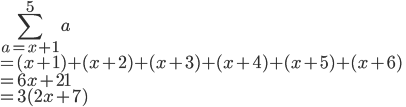
I know it's going to be wrong sir, but I honestly don't have any other clue what else it could be?
Thanks again sir 🙂
Yousuf.
You are so close, but you can't seem to accept the idea of a variable number of terms. You also need to finish with the number at the top.
OK - try these. (And please, DON'T write out every term!!, and don't worry about finding a final answer as a single number. We are only interested in the expansion.)
Hi again sir
I still don't get them sir, the ones for
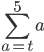
(and the one with x) and also the one with
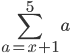 .
.
The ones above should be ...
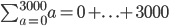
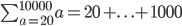
and also
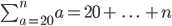
... shouldn't they??
Thanks again sir 🙂
Yousuf.
CORRECT!! All 3 of these are correct. Now we are getting somewhere.
In the first 2 examples (up to 3000 and up to 10000) we know how many terms there are but write "..." to indicate the pattern keeps going UP TO the end number.
In the 3rd one, it finishes with "n". We don't know how many terms there are, but the "..." just means keep going up to n. We don't know what n is - we need more information to find it.
Now it's the same deal when we don't know what the STARTING value is. We just start with that value involving x (like you did successfully above), do a few terms, THEN PUT "..." to indicate missing terms, then FINISH WITH THE TOP NUMBER (which in most of the above examples was 5.)
Now, would you like to try those expansions with x in them again?
Hi again sir
Thanks for reading this and apologies for not having replied back sooner.
Right, I may get this wrong again sir, but does the following expand to...
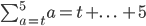
and
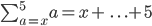
Sorry sir, but I'm convinced the above are incorrect, but I've drawn from the previous principle.
I'm not quite sure if there is a pattern involving the first number (a = t or a = x) so I've assumed we start off with the first number as t or x and proceed therewith to the final number in the sequence, in both cases 5.
Thanks again sir for your kind help and support 🙁
Yousuf.
Hi again
You've got the first and last terms CORRECT!
Let's go back to this example. The proper expansion should have the first few terms and the last few terms, with "..." in the middle, like this:
So try these again, but put in at least 3 terms before the "..." and 3 terms after.
Hi again sir
Thanks for replying back sir.
Oh right, so would they be ..
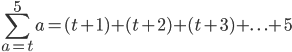
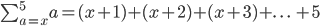
Sir I know you might be thinking I've cheated above to not have put any values before 5 in each instance! But I'm not sure what goes after the "+...+". I was going to write t+n and x+n where n could be any number but haven't done so in knowing it's going to be wrong sir!!
I know from the expressions that ...
-
The first term we start off with is t
-
The terminating term would be 5
-
The sequence follows the natural numbers i.e. 1, 2, 3, 4 ...
However, because a is an unknown value in both instances, we don't know what the number is so we start off with that and because the pattern follows natural numbers, we add 1 onto each consecutive term - until we reach the ending term of 5.
So I'm not 100% sure if we do use the term (a + t) or (a + x) before the 5 in this sir!
Thanks again sir and I'm sorry if it's frustrating!!! 🙂
Yousuf.
Look at my 3000 example above to know what to do after the "..."! That's why I did it.
Why are you now starting with (t+1) and (x+1), when the start values should be t and x??
Hi again sir
Sorry sir that's another silly mistake!
Right so should it be ...
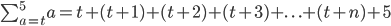
The reason why I've put in (t+n) is because t is a variable value and we can't say whether it's a fixed numeric value.
I think the reason why we can write
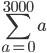
in a way to exemplify 3 starting terms and the last 3 terminating terms including the final term is because a has a fixed value whereas in the expanded example, a is a variable value and could be any number so I can't work out sir how we can use three terms to exemplify the pattern before the final term.
I'm sorry again sir because using a variable initial value in these kind of sequences is something I've come across just recently (well actually on this question in particular!)
Thanks again sir and I'm sorry again for the inconvenience 🙁
Yousuf.
Please look at my 3000 example from before. There is no "n" in it. If the last number is 3000, then the numbers leading up to it will be
... + 2998 + 2999 + 3000,
like I wrote. Now the numbers before 5 will be?? There certainly won't be an "n" in there.
You have the beginning correct, now.
Continuation of this exchange...
See the rest of this discussion here:
See the 10 Comments below.