Life expectancy and semi-log graphs
By Murray Bourne, 23 Oct 2008
How long to you expect to live? What's the probability that you'll be alive tomorrow? Next week? In 10 year's time?
Of course, there are many factors that affect your life expectancy, including how much you smoke, whether you exercise regularly, what your diet is like and how much you stress yourself out.
Life insurance is something you need if you have a family who would suffer financially if you were gone. Life insurance companies need to know the probability of having to make a payout and this affects how much you need to pay for life insurance (or whether they will insure you at all).
There are some key issues that life insurance companies take into consideration. For example, they will ask you whether you smoke. Also, there is often a "13 month exclusion period" in case you are buying the insurance after some traumatic event and they are worried you are a suicide risk (they figure if you survive the event and the anniversary of the event, then you are probably not a bad risk).
Other than that, the insurance companies base their premiums (the amount you have to pay) on life tables. These are simply a list of probabilities that you will be alive in one year from now, given your current age. Here is an extract from the Life Tables Australia. It describes what happens for 100,000 babies born today - the number of them expected to be still alive at various ages and the proportion of those surviving, having made it to a certain age. It also shows the number of years the person is expected to live for, given they have survived to that age.
| Age | No. Alive | Proportion Dying | Years to live |
|---|---|---|---|
| 0 | 100000 | 0.00542 | 78.5 |
| 1 | 99458 | 0.00046 | 77.9 |
| 2 | 99412 | 0.00025 | 76.9 |
| 3 | 99387 | 0.00021 | 75.9 |
| 4 | 99366 | 0.00018 | 75.0 |
| 5 | 99348 | 0.00016 | 74 |
| 6 | 99332 | 0.00014 | 73.0 |
| 7 | 99319 | 0.00012 | 72.0 |
| 8 | 99306 | 0.00012 | 71.0 |
| 9 | 99295 | 0.00011 | 70.0 |
| 10 | 99284 | 0.00011 | 69.0 |
| 20 | 98882 | 0.00083 | 59.2 |
| 30 | 98082 | 0.00102 | 49.7 |
| 40 | 96946 | 0.00149 | 40.2 |
| 50 | 94929 | 0.00304 | 31.0 |
| 60 | 90588 | 0.00765 | 22.2 |
| 70 | 79890 | 0.02090 | 14.4 |
| 80 | 55832 | 0.06012 | 8.2 |
| 90 | 19171 | 0.17027 | 4.2 |
| 100 | 1340 | 0.30799 | 2.5 |
I wanted to see what this looks like visually, so I graphed the "proportion dying" column using Excel.
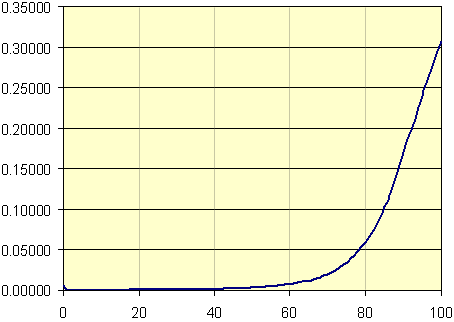
We can't see what's happening before age 40 (it's too flat) and there is an interesting 'blip' at birth that intrigued me. This called for a semi-log graph. I have used a vertical log scale (for "proportion dying" and a linear horizontal ("age") scale.
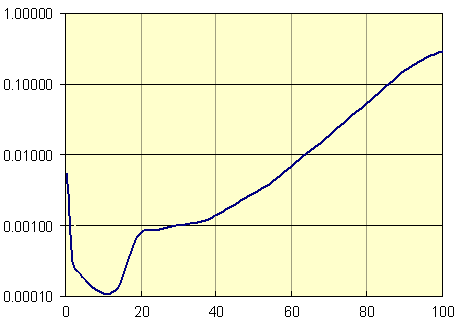
This shows that it is quite a struggle for babies to survive their first year of life. The proportion dying in the first year is about the same as the proportion dying at age 56.
Notice also that the 'safest' period is when we are around 7 to 12 years old. Then when the hormones start racing in the teen years, our 'danger quotient' increases considerably. This is when the brain's frontal lobes are struggling to mature. When we hit 20 years-old, the slope of the graph suddenly reduces. Is this yet another argument for not giving teenagers a drivers license until after age 20?
The semi-log graph has given us a lot more information than the normal linear graph.
Life Tables Australia is an Excel file that you can play around with.
See the 1 Comment below.
