IntMath Newsletter: Spherical spiral, calculators
By Murray Bourne, 20 May 2015
20 May 2015
In this Newsletter:
1. How to find the length of a spherical spiral
2. Resource: EasyCalculation
3. More on Spirals
4. Math puzzles
5. Math movie: How to land on a comet
6. Final thought: The math narrative
1. How to find the length of a spherical spiral
 |
How do we find the length of rope wound around a ball, with equidistant spirals? Here's the solution to an interesting reader's question. |
2. Resource: EasyCalculation
EasyCalculation.com has an amazing variety of online calculators, including not only the usual areas and angles, but also:
- Vector addition, angles and magnitude
- Chemistry (atomic mass, acids and bases)
- Finance
- Date and day
- Color converters (HEX, RGB and CSS)
- Mortgage and other finance related calculators
- Matrix operations
This free offering is a useful resource.
3. More on Spirals
I came across some interesting spiral examples while thinking about Anne's rope and sphere problem.
(a) Escher's Art
 |
Famous artist M. C. Escher used a spherical spiral in the piece Sphere Surface with Fish. The spiral in this image is like my first attempt at solving Anne's problem. See this, and other mathematical art by Escher here: |
(b) Music and spirals
Ever wondered why we use the notes we do in music? The 12 notes we have in an octave (7 white, 5 black on a piano) are no accident. They naturally occur as harmonics in nearly every note we hear.
For example, if we play the note A = 220 Hz on a piano, we also hear a mix of higher notes. We may not be aware of it, but those harmonics are what makes the difference in tone between a cello, a double bass, a bassoon and a pipe organ all playing the same note.
That A note on the piano also includes the following sounds, in various proportions:
- A one octave higher (440 Hz)
- E above that (659.3 Hz)
- A above that (880 Hz)
- C# above that (1108.7 Hz)
And so on, making up what is called the Harmonic Series. You may recognize the major chord A C# E A in these notes. (Different instruments when playing the same note include different proportions of these harmonics, hence producing different tones.)
 |
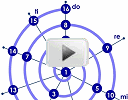This video illustrates this concept of harmonics contained within a musical note via the use of a spiral. Octave spiral with the first 16 elements of the harmonic series |
(c) Ribbon Bodies
 |
Escher also used spirals in his other artworks, including interpretations of clocks and human faces in the form of ribbons. Here's an image inspired by this approach: |
4. Math puzzles
The puzzle in the last IntMath Newsletter asked about the surface area of a tetrahedron.
Correct answers with explanation were given by Sachin and Charles. It was great to see that Sachin made use of the mathematics entry possibilities in his answer.
New math puzzle
Just after Anne's mail came in about the length of a spherical spiral (article above), I came across the following problem, which can also be done in at least 2 very different ways.
We have a cylnder with circumference 3 cm and height 12 cm. A piece of string is wound around the cylinder 4 times, as shown.
What is the length of the string?
Leave your responses here.
5. Math movie - How to land on a comet (Fred Jansen)
 |
How do you align with a tiny rotating comet 600 million km away, travelling at 100,000 km/h, then land on it? This interesting TED talk has some insights into the mathematics behind the problem. |
6. Final thought - The math narrative
I'm lucky to live in a country (Singapore) where the prime minister is a math major.
Lee Hsien Loong studied mathematics at Trinity College, University of Cambridge. He shares the Trinity alumni list with Isaac Newton, James Clark Maxwell, Srinivasa Ramanujan, Charles Babbage, and Niels Bohr.
Lee did so well in his studies that he was named "senior wrangler", which means he was the top mathematics undergraduate, once regarded as "the greatest intellectual achievement attainable in Britain."
He recently posted his code to solve sudoku puzzles on Facebook, earning responses like "cool", "awesome" and "amazing".
When your leaders regard STEM subjects as vitally important to a country's future, it's not surprising the resources and encouragement follow. It's also not surprising how well the country does in international mathematics competitions. The consistent narrative in the country has emphasized the importance of science, mathematics and engineering.
I think it's tragic that so many world leaders are almost "anti-science", and doing very little about the environmental and other serious challenges we're facing.
Other notable persons with a mathematics background are:
- Corazon Aquino (former President of the Philippines)
- Alberto Fujimori (former President of Peru)
- Florence Nightingale (applied statistics to public health; invented the pie-chart)
- Lewis Carroll (author of Alice in Wonderland)
Until next time, enjoy whatever you learn.
See the 9 Comments below.
