IntMath Newsletter: Forum, pistons, Shodor
By Murray Bourne, 26 Jan 2016
26 Jan 2016
In this Newsletter:
1. New: IntMath Forum
2. Piston curve
3. Resource: Shodor Interactivate
4. Math puzzles
5. Math movies: Misleading statistics
6. Final thought: Resolutions, 1% at a time
1. New: IntMath Forum
A lot of people have asked for a forum over the years. Finally, it's here!
I come across too many low quality forums and I'm hoping to avoid that. I also get a lot of mails containing math homework questions where the writer just wants me to provide the answer. This doesn't help him learn much - it just helps his marks. So there are 5 simple principles for the forum:
Principles of the IntMath Forum
You can enter math in the forum using simple plain text (or LaTeX if you prefer). You can also add graphs and images to your post. Details on how to do so can be found here:
How to enter math, graphs and images
Wanted: Volunteer Tutors
The forum needs tutors that embrace the 5 Principles mentioned above. That is, tutors should firstly be confident in answering the question, but help readers figure out problems by themselves, not just do it for them. The best help is given by prompting, reminding, and asking good questions - not simply providing the answer.
To get an idea what I mean, see these exchanges where I'm pointing the user to relevant resources, and asking questions. Eventually, they work it out:
- Graphing a Fish Population Word Problem
- Lowest common denominator
- Prove the trig identity cosx/(secx+tanx)= 1-sinx
Let me know (by replying to this mail, or in the comments) if you are interested to be a tutor.
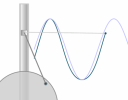
2. Does a piston follow a sine curve shape?
 |
In the Trigonometric Graphs section, I used a piston example for one of the sine curves. A reader pointed out that a piston does not exactly follow a sine curve at all. Here's a short article with an interactive animation that explores this issue: |
3. Resource: Shodor's Interactivate
 |
I've been a fan of Shodor's Interactivate for many years. Indeed, it helped to inspire IntMath. Their activities used to be java-based, and so didn't work on mobile devices. But now, their interactive activities are mobile friendly. See over 300 activities, covering algebra, functions, ciphers, calculus, and probability here: |
4. Math puzzles
The puzzle in the last IntMath Newsletter asked about the ratio of the areas of Reuleaux Triangles.
Correct answer with explanation was given by Stephen, who was also was one of the few to express the final answer as a ratio, as required.
New math puzzle
The length of a rectangle increases by 10% and the width decreases by 10%. Which of the following is true?
- The area does not change.
- The area becomes smaller or larger depending on the original lengths of the sides.
- The area will always become smaller.
- The area will always become larger.
You can leave your responses here.
5. Math movie: Misleading statistics
 |
This video outlines Simpson's Paradox, which all budding statisticians need to be aware of. This is part of a TED-Ed lesson. |
Related article: Misleading charts
Around the same time I watched How statistics can be misleading, I came across the following article on Quartz.
I feel it's a vital mathematical skill to be able to properly analyze data, especially when it's in visual form.
I don't agree with all the writer's suggestions, but overall it's quite a good analysis:
The most misleading charts of 2015, fixed
6. Final thought: Resolutions, 1% at a time
You probably made new year resolutions and now that life has taken over, maybe they've been shelved already.
A possibly more effective and realistic way of challenging yourself to improve is to aim for 1% improvement per day (or some other reasonably short time frame). If you want to exercise more, try just walking (or running, or any other exercise) 1% more than the day before. This will mean you'll double your walking distance in just 70 days:
(1.01)70 = 2.007
You could apply a similar small and realistic improvement goal for your studies: say 5% improvement for each weekly test.
Either way, all the best achieving your goals in 2016!
Until next time, enjoy whatever you learn.
See the 17 Comments below.
