Interesting semi-logarithmic graph - YouTube Traffic Rank
By Murray Bourne, 25 Jan 2007
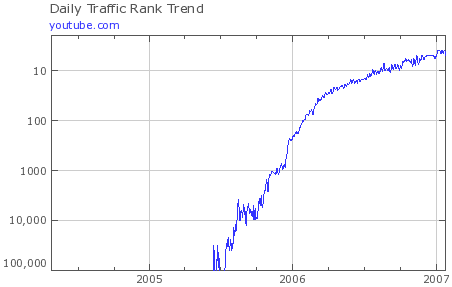
The growth in popularity of YouTube has been extraordinary. It has gone from an unknown, unheard-of site (not even in the top 100,000 sites, so off the scale) to the 5th highest ranked site on the Web, all in the space of 18 months.
This image, from Alexa, is an interesting example of a semi-logarithmic graph. The vertical scale (traffic rank) is logarithmic, while the horizontal scale (time) is linear.
See the 7 Comments below.
